题目中说明对于一个数字n,有如下定义:
唯一分解定理: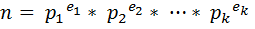
σ 函数的定义如下:
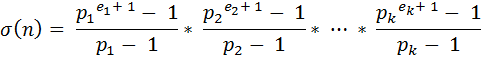
现在给出一个n ( 1 <= n <= 10^12 ),问在1到n中有多少个整数k使得 σ(k) 为偶数 ?
我们先观察上述式子,发现要想让σ(n)为偶数,那么只要其中有一项 (1 <= i <= k )为偶数即可,
(1 <= i <= k )为偶数即可,
我们可以将这个式子变型一下,分子部分可以变为:![]() ,约去分母就变为
,约去分母就变为![]() ,
,
我们可以观察这个式子,我们知道pi都是素数,素数除了2以外都是奇数,所以前面的式子是奇是偶决定于ei的大小,若ei为奇数,就相当于奇数个奇数(若pi不是2,那么![]() 肯定是奇数)相加,和是个奇数,再加上1就变成偶数了,反之,若ei为偶数,就相当于偶数个奇数相加再加1,和就是奇数了。如果pi刚好就是2的话,那么上述约去分母之后的式子就是许多偶数相加再加1,这就是个奇数,这个是对σ(n)为偶数没有任何贡献的,所以我们可以直接忽略。
肯定是奇数)相加,和是个奇数,再加上1就变成偶数了,反之,若ei为偶数,就相当于偶数个奇数相加再加1,和就是奇数了。如果pi刚好就是2的话,那么上述约去分母之后的式子就是许多偶数相加再加1,这就是个奇数,这个是对σ(n)为偶数没有任何贡献的,所以我们可以直接忽略。
所以我们得出结论:对于n,若将n进行唯一分解之后,如果存在任何一个 pi != 2 且 ei ( 1 <= i <= k )为奇数则 σ(n) 为偶数。
现在需要求的是计算1-n之间能让σ(k)为偶数的k的个数。这个有些复杂,因为我们上面说到是有任意一个ei为奇数就可以判出对应的σ值为偶数,这种情况太多太多了,所以我们考虑这个问题的反面:我们求出1-n之间能让σ(k)为奇数的k的个数,这个符合条件的k是很少的(从样例中就能看出来,1000以内能使得σ(k)为奇数的k才53个)。
若σ(n)为奇数,则每一项 都必须为奇数,意味着每一项约分之后的
都必须为奇数,意味着每一项约分之后的![]() 都必须为奇数,也就是说每一项的ei都必须是偶数,也就是说n必须为平方数。但是这里有个小问题前面证明过当pi为2时,无论ei是什么,这一项都是奇数。这些平方数乘以2之后,其σ也是奇数(读者可能会问:如果再乘以2呢?其实这就是另一个平方数了,所以我们只需要考虑乘以一个2即可)。
都必须为奇数,也就是说每一项的ei都必须是偶数,也就是说n必须为平方数。但是这里有个小问题前面证明过当pi为2时,无论ei是什么,这一项都是奇数。这些平方数乘以2之后,其σ也是奇数(读者可能会问:如果再乘以2呢?其实这就是另一个平方数了,所以我们只需要考虑乘以一个2即可)。
所以我们就有了这样的结论:若n为平方数,或为平方数的2倍,那么σ(n)为奇数。
我们现在的任务就是生成上述两种数,这个好办,小于n的平方数为sqrt(n)个,这些平方数的2倍的个数是sqrt(n/2)。所以我们的程序很简单:
1 #include2 using namespace std; 3 4 typedef long long LL; 5 typedef unsigned long long ULL; 6 7 int main(){ 8 int T; 9 scanf("%d", &T);10 for(int ca = 1; ca <= T; ++ca){11 LL n, m;12 scanf("%lld", &n);13 m = (LL)sqrt(n+0.5) + (LL)sqrt(n/2+0.5);14 printf("Case %d: %lld\n", ca, n-m);15 }16 return 0;17 }